Cours - Programmation dynamique

La programmation dynamique, conçue dans les années 1950 par le mathématicien américain Richard Bellman, partage une similitude avec la méthode « diviser pour régner ». Elle consiste à décomposer un problème complexe en sous-problèmes plus simples, puis à utiliser ces derniers pour trouver la solution optimale au problème initial. La principale différence réside dans l'utilisation de la « mémoïsation », qui implique l'enregistrement des résultats intermédiaires des sous-problèmes dans un cache afin d'éviter leur recalcul ultérieur.

La programmation dynamique est applicable lorsque deux conditions sont réunies :

• Sous-structure optimale : Un problème a une sous-structure optimale s’il peut se décomposer en sous-problèmes et si sa solution optimale peut se calculer à partir de la solution optimale de ses sous-problèmes. En d'autres termes, toute étape doit pouvoir être calculée à partir des étapes précédentes. Généralement, cela signifie que la résolution du problème peut se représenter à l’aide d’un graphe.
• Sous-problèmes superposés : Un problème satisfaisant cette condition nécessite de résoudre plusieurs fois le(s) même(s) sous-problème(s). En d’autres termes, sa résolution ne doit pas pouvoir se représenter comme un arbre.

Méthodes ascendante et descendante

On distingue deux façons de calculer une solution en utilisant la programmation dynamique : la méthode ascendante (bottom-up en anglais) et la méthode descendante (ou top-down).

• La méthode ascendante consiste à partir des plus petits sous-problèmes et d'enregistrer leurs résultats pour résoudre les problèmes plus grands, et ainsi de suite jusqu’à résoudre le problème global. La mémoïsation des résultats intermédiaires s’effectue donc de bas en haut (bottom-up), en partant des problèmes les plus simples jusqu'aux plus complexes.
• Dans la méthode descendante, on part du problème initial et on procède de façon récursive, mais en enregistrant les valeurs déjà calculées afin de ne pas résoudre le même sous-problème plusieurs fois.

Exercice - Fibonacci

On rappelle l'algorithme de Fibonacci écrit de manière naïve :

def fibonacci(n):
    ''' Renvoie le n-ième terme de la suite de Fibonacci
    :param n: (int) indice du terme à calculer
    :return: (int) n-ième terme de la suite '''

    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

Si l'on représente l'arbre des appels récursifs pour fibonacci(4) par exemple, on obtient ceci:

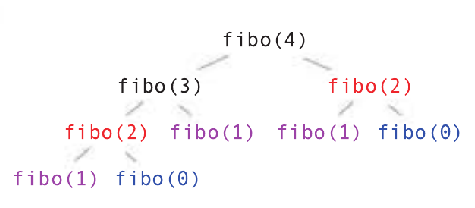
Approche descendante :

Dans la méthode descendante (top-down), on part du problème initial et on procède de façon récursive, mais en enregistrant les valeurs déjà calculées (avec la mémoïsation) afin de ne pas résoudre le même sous-problème plusieurs fois.

On va donc créer une liste de mémoïsation mem. Cette liste n’est pas remplie dans l’ordre croissant et on ne peut donc pas utiliser la méthodeappend() au fur et à mesure. Elle doit être initialisée avec le nombre total de « cases » qu’elle devra contenir.

def fibonacci(n, mem):
    ''' Renvoie le n-ième terme de la suite de Fibonacci
    :param n: (int) indice du terme à calculer
    :param mem: (list[int]) tableau de mémoïsation
    :return: (int) n-ième terme de la suite '''

    if mem is None : # Premier appel, on initialise notre « cache »
        mem = [None] * (n +1) # Un tableau contenant n+1 fois `None`
    if mem[n] is None:
        if n <= 1:
            ...
        else:
            ...
    return ...

Approche ascendante :

Dans la méthode ascendante, on part des plus petits sous-problèmes et on enregistre leurs résultats pour résoudre les problèmes plus grands, et ainsi de suite jusqu’à ce que l’on ait résolu le problème global. La mémoïsation des résultats intermédiaires s’effectue donc de bas en haut (bottom-up), en partant des problèmes les plus simples.

def fibonacci(n, mem):
    ''' Renvoie le n-ième terme de la suite de Fibonacci
    :param n: (int) indice du terme à calculer
    :param mem: (list[int]) tableau de mémoïsation
    :return: (int) n-ième terme de la suite '''

    mem = [] # Notre « cache » de mémoïsation
    mem.append(0) # fibonacci(0) = 0
    mem.append(...) # fibonacci(1) = 1

    for i in range(..., ...):
        mem.append(...)
    return ...