Le tri par insertion

Nous avons vu la méthode de tri par sélection, qui a l'avantage d'être facile à appréhender, mais qui s'avère être fortement coûteuse (coût quadratique dans tous les cas).
Voyons s'il n'existe pas d'autres algorithmes de tri plus intéressants.

Présentation du tri par insertion

Avec un jeu de cartes

Le tri par insertion est un autre algorithme de tri par comparaisons, dont le principe est un peu différent, mais plus "naturel".

Dans cette partie, on verra comment trier une suite de cartes en utilisant la méthode de tri par insertion. On utilisera l'ordre suivant (de la carte la plus faible à la plus forte) :

Note : Si vous avez une carte Joker dans votre jeu, on considèrera qu'elle est plus forte que toutes les autres cartes.

Activité préliminaire

Munissez-vous d'un paquet de carte, mélangez-le, et placez-le en face cachée.
Vous disposez d'une zone de jeu dans laquelle vous ajouterez les cartes une par une, de manière à toujours avoir une suite de cartes triée.
L'objectif est de trier les 7 premières cartes du paquet.

• Prenez la première carte du paquet et posez-la (face visible) dans votre zone de jeu.
  La suite de cartes de votre zone de jeu (composée pour le moment d'une seule carte) est-elle triée ?
• Prenez la deuxième carte du paquet, et intégrez-la à votre suite de cartes de manière à ce que celle-ci reste triée.
• Prenez la troisième carte du paquet et faites de même. Répétez cela jusqu'à avoir une suite de 7 cartes triées dans votre zone de jeu.

Question : Décrivez la méthode que vous avez suivi pour intégrer chaque nouvelle carte à votre suite de cartes triée.

---

Voici le déroulement de la méthode de tri par insertion sur une suite de cartes.
On souhaite trier la suite de cartes suivantes :

Une suite de 5 cartes.

Composition du tableau

On distingue deux parties dans le tableau :

• une partie triée (en vert), initialement composée de la première carte.
• une partie non-triée (en gris), initialement composée du reste des cartes.

On dispose également d'une zone mémoire dans laquelle peut placer une carte temporairement.

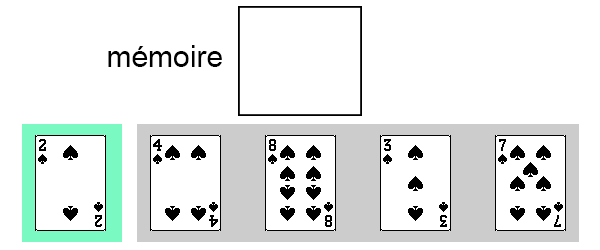
On commence donc par traiter la deuxième carte du tableau, qui est la première carte de la partie non-triée. On place cette carte dans la zone mémoire.

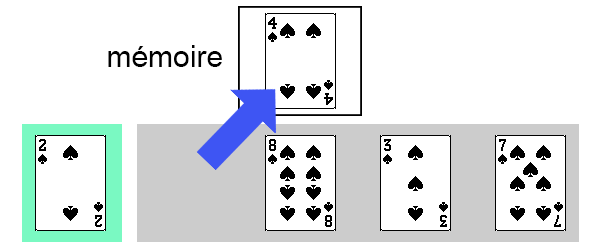
Ensuite, on procède comme suit :

Placer la carte à sa bonne position

• En partant de la carte positionnée juste à gauche de celle que l'on cherche à trier (c'est-à-dire la dernière carte de la partie triée du tableau), et en allant jusqu'à la première carte du tableau :
  • On décale d'une position à droite chaque carte dont la valeur est strictement supérieure à la carte que l'on cherche à replacer.
  • On s'arrête uniquement si la carte n'a pas une valeur supérieure, ou si l'on a parcouru toutes les cartes.
• On replace la carte (actuellement en mémoire) à sa bonne position.

Ici, la carte qui précède celle à replacer (qui se trouve en mémoire) est inférieure à la carte à replacer. Cela signifie que notre carte est déjà à sa bonne position.

Il n'y a donc pas de décalage à faire, et on replace la carte à sa position initiale.

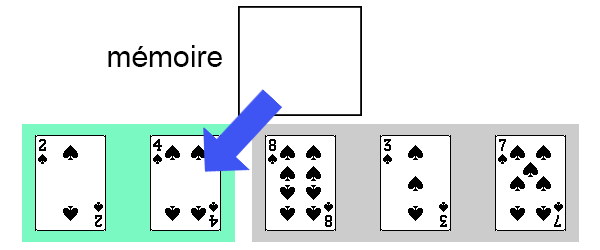
La partie triée de notre tableau est maintenant composée des deux premières cartes.

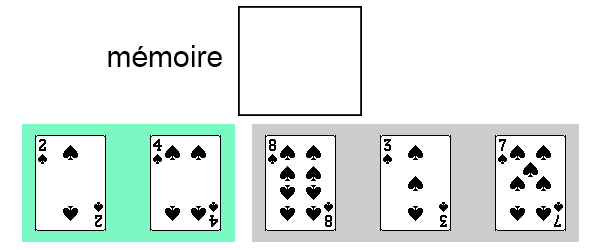
On fait de même avec la troisième carte du tableau (première carte de la partie non-triée).

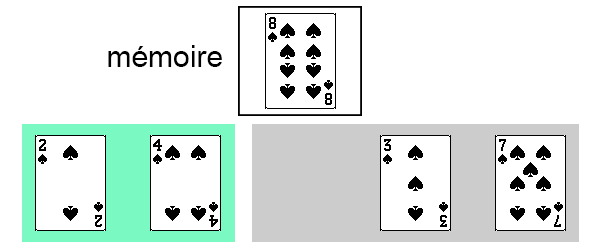
Ici encore, la carte était déjà à sa bonne position.

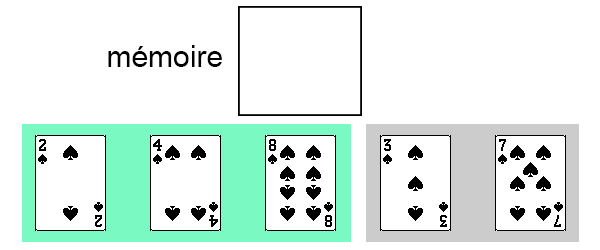
On a maintenant 3 cartes dans la partie triée du tableau.
On met la quatrième carte (de valeur 3) en mémoire.

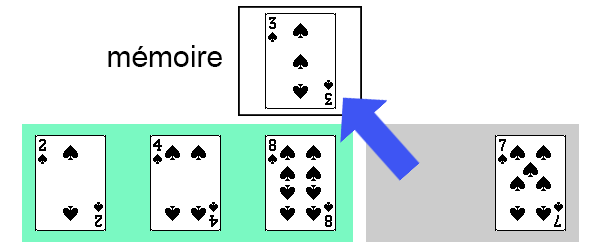
On constate que les deux cartes précédentes (de valeurs 8 et 4) ont une valeur supérieure à celle de la carte que l'on souhaite trier. Il faut donc déplacer à droite ces deux cartes.

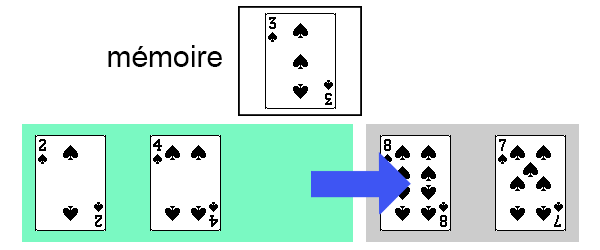
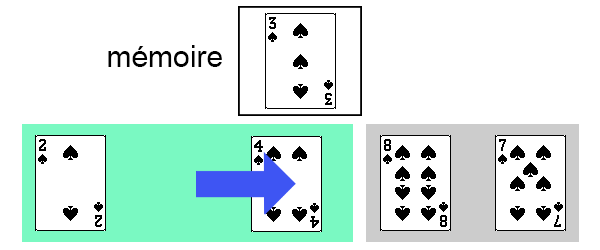
On peut maintenant repositionner notre carte.

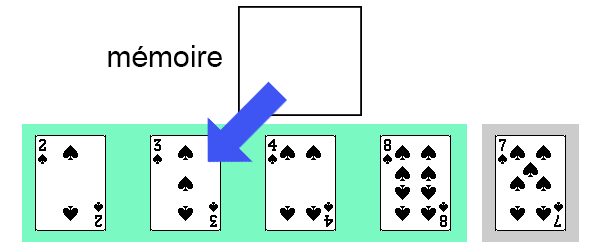
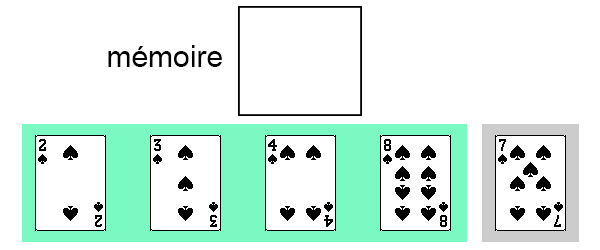
Il ne reste ainsi plus qu'une seule carte dans la partie non-triée de notre tableau.

On répète le même principe, on place cette carte en mémoire.

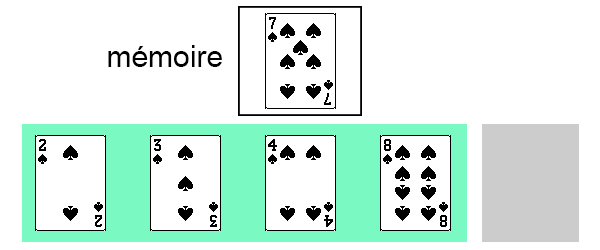
Ici, il n'y a que la carte précédente à déplacer.

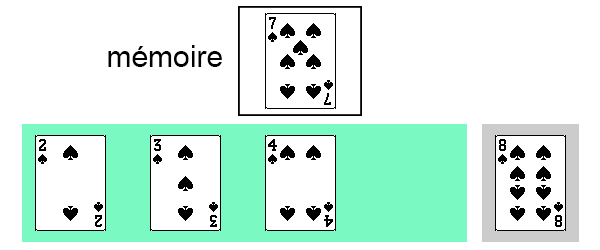
Puis on repositionne notre carte.

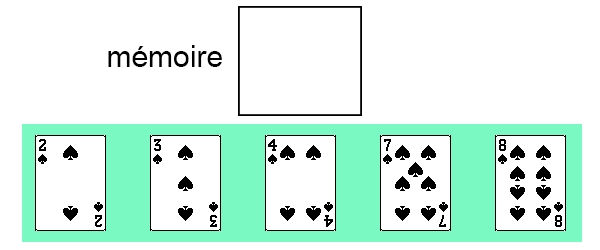
Et voilà, on vient de trier une suite de 5 cartes par la méthode de tri par insertion !

À vous de jouer

Disposez une suite de 7 cartes choisies au hasard dans un paquet de cartes.
Votre zone de jeu est composée de votre suite de cartes et d'un emplacement mémoire.
Effectuez le tri de votre suite de cartes en utilisant la méthode de tri par insertion présentée ci-dessus.

Trier un tableau

On a donc vu que la méthode de tri par insertion avait l'avantage d'être assez naturelle, raison pour laquelle elle est souvent utilisée pour trier des cartes à jouer.

Appliquons à présent ce tri sur des tableaux d'entiers.

On rappelle le principe du tri par insertion :

• on fait comme si les éléments de la partie non-triée du tableau étaient donnés un par un, le premier élément du tableau constituant, à lui seul, un tableau triée de longueur 1,
• on y range ensuite le deuxième élément du tableau pour constituer un tableau trié de longueur 2,
• puis on y range le troisième élément pour obtenir un tableau trié longueur 3,
• et ainsi de suite jusqu’à avoir traité le dernier élément...

On insère donc à la n^ième itération le n^ième élément à sa bonne position en décalant à droite tous les éléments de la partie triée du tableau qui lui sont supérieurs.

Exercice - Trier un tableau

On souhaite trier le tableau suivant avec le tri par insertion : [5, 3, 1, 4, 6, 2].
Indiquez quel est l'état du tableau après chaque insertion d'élément.

Source : http://fractale.gecif.net/nsi/pdf/cours/algorithmes/algo_tri.pdf

Faites de même avec le tableau [2,8,1,5,2,3].

L'algorithme

Présentation de l'algorithme

Note

Dans la partie précédente, on a souvent parlé de "déplacements" de cartes. En machine, ces déplacements seront implémentés sous la forme de copies d'éléments, en réalisant des affectations.

Algorithme du tri par insertion

ALGORITHME : tri_insertion
ENTRÉE :
  tableau : un tableau d'éléments
SORTIE : aucune (tri en place)

DÉBUT
  POUR i ALLANT DE 1 À longueur(tableau) - 1
    cle ← tableau[i]
    j ← i \(-\) 1
    TANT QUE j ≥ 0 ET QUE tableau[j] > cle
      tableau[j + 1] ← tableau[j]
      j ← j \(-\) 1
    FIN TANT QUE
    tableau[j + 1] ← cle
  FIN POUR
  Renvoyer ∅
FIN ALGORITHME

Exercice 1

Déroulez l'algorithme sur le tableau [5, 3, 1, 4, 6, 2].

Exercice 2

1. Pourquoi commence t-on la boucle POUR à partir de 1 ?
2. Expliquez à quoi sert la 3^ème ligne de l'algorithme : j ← i - 1.
3. Dans le TANT QUE, à quoi sert la première condition j ≥ 0 ? La deuxième condition tableau[j] > cle ? Pourrait t-on inverser les deux conditions ?
4. À quoi sert la ligne tableau[j + 1] ← tableau[j] dans le TANT QUE ?
5. Pourquoi décrémente t-on (c'est-à-dire que l'on diminue de 1) la valeur de j à chaque tour de la boucle TANT QUE ?
6. Expliquez l'affectation tableau[j + 1] ← cle après la boucle TANT QUE.

Tri stable

Le tri par insertion, écrit comme ci-dessus, est dit "stable" car, en cas de valeurs identiques dans le tableau initial, leur ordre relatif n’est pas modifié.

Une petite animation

Simulation du tri par insertion

En vert : éléments déjà triés
En gris : éléments à trier

Espace mémoire:

Lancer le tri Pas à pas

Implémentation en Python

Maintenant que l'on a déterminé l'algorithme du tri par insertion, on peut l'implémenter en Python.

Téléchargez le programme squelette (à compléter) ci-dessous.

Fichiers Python

• tri_insertion.py : programme Python avec les fonctions à compléter.
• (à venir) : programme Python corrigé.

Module doctest

Dans la docstring de la fonction tri_insertion, des tests sont présents. Ces tests sont exécutés par le module natif doctest. Lorsque vous exécutez le programme, si les tests réussissent, rien ne se passera. Sinon, vous obtiendrez des informations sur les tests qui ont échoué.

La fonction testmod (qui exécute les tests) est appelée dans la dernière ligne du programme. Pour obtenir davantage d'informations sur les erreurs liées aux tests, vous pouvez activer le mode verbeux en remplaçant le paramètre verbose=False par verbose=True.

Exercice préliminaire

Dans les tests présents dans la docstring de la fonction tri_insertion, la première instruction est la suivante :
>>> l = [randint(0, 99) for _ in range(10)]
Expliquez ce que fait cette instruction.

Exercice 1

Écrivez la fonction tri_insertion. Exécutez le programme pour vous assurer que votre fonction soit correcte (il ne doit rien se passer).

Exercice 2

Écrivez la fonction tri_insertion_decroissant permettant de trier un tableau dans l'ordre décroissant. Que faut-il changer par rapport à la fonction tri_insertion ?

Coût de l'algorithme

Comme pour le tri par sélection, on analysera le coût algorithmique du tri par insertion en comptant le nombre de comparaisons effectuées entre deux éléments du tableau.

Fichier Python

• tri_insertion_comp.py : programme Python permettant de visualiser le déroulement du tri et le nombre de comparaisons effectuées.

Vous n'avez pas besoin de modifier ce fichier en dehors du contenu des deux variables globales :

• TABLEAU : Tableau donné en entrée à la fonction effectuant le tri par insertion.
• MODE_SLEEP : Permet d'activer le mode "pas à pas". En activant ce mode, vous devrez appuyer sur la touche "Entrer" lorsque demandé afin de passer à l'étape suivante. Affectez la variable à True activer ce mode, ou à False sinon.

Exercice 1

Téléchargez le fichier Python ci-dessus.

1. Exécutez ce programme avec un tableau de 5 éléments triés dans l'ordre décroissant. Combien y a t-il de comparaisons :
   • à la première itération (\(i = 1\)) ?
   • à la deuxième itération (\(i = 2\)) ?
   • à la troisième itération (\(i = 3\)) ?
   • à la quatrième itération (\(i = 4\)) ?
   • au total ?
2. Faites la même chose que précédemment avec un tableau de 5 éléments triés dans l'ordre croissant.
3. Selon vous, quel est le meilleur des cas et le pire des cas concernant le tableau donné en entrée de la fonction de tri par insertion ?

Rappel sur les complexités

Voici un rappel sur les différentes complexités :

• Logarithmique \(Θ(log~n)\) : la complexité évolue moins vite que le nombre n de données (par exemple : si on multiplie le nombre de données n par 2, on ne rajoute qu'une seule opération).
• Linéaire \(Θ(n)\) : la complexité évolue comme le nombre n de données (par exemple : si on multiplie le nombre de données n par 2, le temps d'exécution est multiplié par 2).
• Quasi-linéaire \(O(n~log~n)\) : Intermédiaire entre linéaire et quadratique. En pratique, un algorithme de complexité quasi-linéaire a un comportement très proche d’un algorithme de complexité linéaire.
• Quadratique \(Θ(n^2)\) : la complexité évolue comme le carré du nombre n de données (par exemple : si on multiplie le nombres de données n par 2, le temps d'exécution est multiplié par 4).
• Exponentielle \(Θ(2^n)\) : la complexité évolue à terme beaucoup plus vite que n'importe quelle fonction polynomiale du nombre n de données (par exemple : si on multiplie le nombre de données n par 100, le temps d'exécution est multiplié par \(2^{100}\), soit 1267650600228229401496703205376).

Courbes d'évolution des différentes complexités algorithmiques.
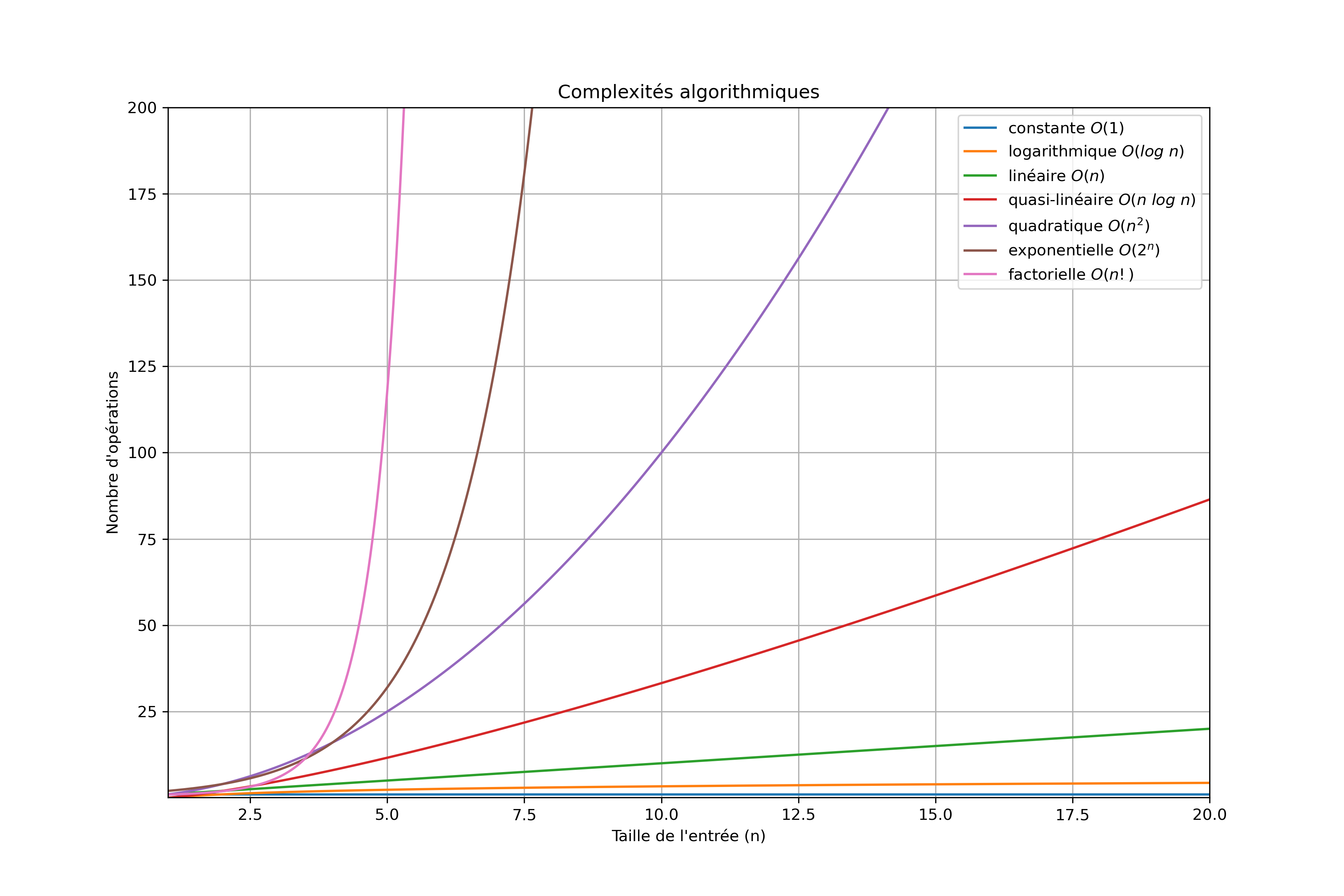
(généré avec ce programme)

Exercice 2

Exécutez le programme avec des tableaux triés dans l'ordre croissant de différentes longueurs. Pour une longueur \(n\) donnée, quel sera le nombre \(C(n)\) de comparaisons obtenu dans le cas où le tableau est trié dans l'ordre croissant ?

En déduire le coût du tri par insertion dans le meilleur des cas (logarithmique ? linéaire ? quasi-linéaire ? quadratique ? exponentiel ?).

Exercice 3

Exécutez le programme avec des tableaux triés dans l'ordre décroissant :

• de longueur \(5\),
• de longueur \(6\),
• de longueur \(7\).

On notera le nombre de comparaisons sous la forme \(C(n) = C_i(1) + C_i(2) + [...] + C_i(n-2) + C_i(n - 1)\) avec \(n\) la longueur du tableau et \(C_i(i)\) le nombre de comparaisons effectuées à l'itération \(i\).

Pour une longueur \(n\) donnée, quel sera donc le nombre \(C(n)\) de comparaisons obtenu dans le cas où le tableau est trié dans l'ordre décroissant ?

En déduire le coût du tri par insertion dans le meilleur des cas (logarithmique ? linéaire ? quasi-linéaire ? quadratique ? exponentiel ?).

Terminaison du tri par insertion

Pour démontrer la terminaison de notre algorithme, il faut exhiber un variant de boucle pour chacune des boucles de l'algorithme.

Variant de boucle

On appelle variant de boucle toute quantité \(v\) (qui peut être déterminée en fonction des différentes variables du programme) telle que :

• \(v\) ne prend que des valeurs entières,
• \(v\) est initialement positive,
• \(v\) décroit strictement à chaque passage dans la boucle.

On exhibe un variant de boucle pour démontrer qu'une boucle se termine, en un temps fini.
S'il existe plusieurs boucles dans un programme, il faut trouver autant de variants qu'il y en a.

Prouver la terminaison

Concrètement, on peut prouver la terminaison d'un algorithme en montrant que les deux propositions suivantes sont vraies :

• Proposition A : les boucles peuvent s'exprimer sous la forme TANT QUE VARIANT > 0
• Proposition B : le VARIANT est une suite d'entiers strictement décroissante.

Si les deux propositions A et B sont vraies (\(A \land B\)), l'algorithme s'arrêtera toujours. Autrement (au moins l'une des deux propositions n'est pas vérifiée, \(\neg(A \land B)\)), il existe au moins un cas où l'algorithme ne se terminera pas.

Exemple

Démontrons que la boucle POUR suivante se termine :

POUR i ALLANT DE 10 à 49 AVEC UN PAS DE 5:
    Instructions ne modifiant pas la valeur de i...

On peut ré-écrire cette boucle POUR avec une boucle TANT QUE :

i = 10
TANT QUE i < 50:
    Instructions ne modifiant pas la valeur de i...
    i = i + 5

Si on note \(n\) le nombre de tours de boucle effectué, on peut représenter les valeurs successives que va prendre \(i\) sous la forme d'une suite arithmétique :
\(i_n = i_0 + r*n\), avec \(i_0\) la valeur initiale de \(i_n\) et \(r\) la raison de la suite.

Ici, \(i_0 = 10\) et \(r = 5\).
Donc \(i_n = 10 + 5n\).

On peut donc ré-écrire la condition TANT QUE de la manière suivante :

TANT QUE \(i_n < 50\)
TANT QUE \(10 + 5n < 50\)
TANT QUE \(0 < 50 - 10 - 5n\)
TANT QUE \(50 - 10 - 5n > 0\)
TANT QUE \(40 - 5n > 0\)

On obtient donc notre variant \(v_n\) qui prend la forme d'une nouvelle suite arithmétique :
\(v_n = v_0 - r*n\) avec \(v_0 = 40\) pour valeur initiale et \(r = -5\) pour raison de la suite.
Donc :
\(v_n = 40 - 5n\) est un variant de la boucle car il s'agit d'une suite d'entiers, initialement positive et qui décroit strictement à chaque tour de boucle (car la raison est négative).

On a trouvé un variant, et donc démontré la terminaison de notre boucle.

On rappelle l'algorithme du tri par insertion :

Algorithme du tri par insertion

ALGORITHME : tri_insertion
ENTRÉE :
  tableau : un tableau d'éléments
SORTIE : aucune (tri en place)

DÉBUT
  POUR i ALLANT DE 1 À longueur(tableau) - 1
    cle ← tableau[i]
    j ← i \(-\) 1
    TANT QUE j ≥ 0 ET QUE tableau[j] > cle
      tableau[j + 1] ← tableau[j]
      j ← j \(-\) 1
    FIN TANT QUE
    tableau[j + 1] ← cle
  FIN POUR
  Renvoyer ∅
FIN ALGORITHME

Exercice 1

Montrer la terminaison de la boucle TANT QUE. Il y a deux conditions qui doivent être vérifiées pour pouvoir rentrer dans la boucle. Si une seule des deux conditions (\(j ≥ 0\) ou \(tableau[j] > cle\)) n'est plus vérifiée, alors la boucle s'arrête.

On ne tiendra compte ici que de la première condition : TANT QUE j ≥ 0.

Exercice 2

Enfin, montrer la terminaison de la boucle POUR principale de l'algorithme.

Correction du tri par insertion

Dans les deux parties précédentes, nous avons montré :

• Le coût algorithmique de l'algorithme du tri par insertion, qui est quadratique dans le pire des cas, c'est-à-dire en \(O(n^2)\), et qui est linéaire dans le meilleur des cas, c'est-à-dire en \(O(n)\).
• La terminaison de l'algorithme. On sait que l'algorithme finira toujours par se terminer.

Il reste toutefois à démontrer que l'algorithme renvoie toujours un résultat correct.

On rappelle que la preuve de correction d'un algorithme permet d'affirmer :

• qu'il fournit toujours la bonne réponse
• sur toutes les entrées valides qu'on lui donne (les entrées qui respectent les préconditions).

Pour démontrer la correction du tri par insertion, il faut déterminer un invariant de boucle pour la boucle principale de notre algorithme.

Invariant de boucle

On appelle invariant de boucle une propriété \(P\) qui est vraie avant et après chaque itération de la boucle.

On rappelle que l'on démontre un invariant en utilisant un raisonnement par récurrence.

Démonstration de l'invariant par récurrence

Pour montrer à l'aide d'une récurrence simple qu'une proposition \(P(k)\) est vérifiée pour tout entier \(k \ge 0\), avec \(k\) le nombre d'itérations de la boucle effectuées :

• Initialisation : on vérifie que la proposition est vraie au rang initial \(0\), c'est-à-dire avant le premier passage dans la boucle.
• Conservation : on suppose que la proposition est vraie à un certain rang \(k \ge 0\) fixé, c'est-à-dire après \(k\) tours de boucle, et on en déduit qu'elle est vraie au rang suivant \(k + 1\), c'est-à-dire après un tour de boucle en plus. On peut écrire \(P_k \implies P_{k+1}\).
• Terminaison : on exploite les deux phases précédentes et on montre que la proposition est vraie sur toutes les données une fois la dernière itération de la boucle effectuée.

---

Dans la cas du tri par insertion, on peut décomposer le problème en :

• un sous-tableau trié à gauche, initialement composé du premier élément,
• un sous-tableau non-trié à droite.

Une proposition d'invariant

On propose l'invariant \(P_k\) suivant : « Après \(k\) tours de boucle, \(k+1\) éléments sont triés dans le sous-tableau \([0;k]\) de gauche. »

Algorithme du tri par insertion

ALGORITHME : tri_insertion
ENTRÉE :
  tableau : un tableau d'éléments
SORTIE : aucune (tri en place)

DÉBUT
  POUR i ALLANT DE 1 À longueur(tableau) - 1
    cle ← tableau[i]
    j ← i \(-\) 1
    TANT QUE j ≥ 0 ET QUE tableau[j] > cle
      tableau[j + 1] ← tableau[j]
      j ← j \(-\) 1
    FIN TANT QUE
    tableau[j + 1] ← cle
  FIN POUR
  Renvoyer ∅
FIN ALGORITHME

Exercice 1 : Initialisation

Commençons par l'initialisation. Avant de rentrer dans la boucle (\(k=0\)), l'invariant \(P_k\) est-il vérifié ?

Réponse 1

Avant de rentrer dans la boucle (k=0), notre sous-tableau trié ne contient que la première valeur. Or, un sous-tableau ne contenant qu'un élément est trié.

\(P_k\) correspond à cette proposition :

« Après \(k\) tours de boucle, \(k+1\) éléments sont triés dans le sous-tableau \([0;k]\) de gauche. »

\(P_0\) correspond donc à :

« Après 0 tours de boucle, 1 élément est trié dans le sous-tableau [0;0] de gauche. »

La propriété \(P_0\) est vérifiée, on a terminé la phase d'initialisation.

Exercice 2

Quelle va être la valeur :

• de \(i\) lors du premier tour de la boucle POUR principale ?
• de \(j\) avant de rentrer dans le TANT QUE lors du premier tour de la boucle principale ?

Indiquez quelle est la relation entre \(k\) et \(i\).

Exercice 3 : Conservation

Démontrons maintenant la conservation, c'est-à-dire que \(P_k \implies P_{k+1}\).
Pour cela, on suppose d'abord vraie la proposition \(P_k\) : « Après \(k\) tours de boucle, \(k+1\) éléments sont triés dans le sous-tableau \([0;k]\) de gauche. »
Il faut maintenant démontrer que la proposition \(P_{k+1}\) est également vraie.

On distinguera pour cela trois cas :

• le cas où la clé (d'indice \(k+1\)) est inférieure à tous les éléments du sous-tableau trié \([0;k]\),
• le cas où la clé (d'indice \(k+1\)) est supérieure à tous les éléments du sous-tableau trié \([0;k]\),
• le cas où la clé (d'indice \(k+1\)) est inférieure à certains éléments du sous-tableau trié \([0;k]\), mais pas tous.

Réponse 3

Au début du tour de boucle \(k+1\) :

• l'indice \(i\) est égal à \(k+1\),
• on dispose d'un sous-tableau \([0;k]\) trié auquel on va rajouter un nouvel élément, la clé d'indice \(k+1\).

Cas 1 : clé (indice \(k+1\)) inférieure aux éléments de [0;k] :

• La boucle TANT QUE continue jusqu'à avoir parcouru tous les éléments du sous-tableau trié, car tous les éléments ont une valeur supérieure à la clé. On décale donc tous les éléments du sous-tableau trié d'une case vers la droite.
  Les éléments de \([0;k]\) sont à présent dans \([1;k+1]\).
• L'ordre des éléments est conservé (on les a seulement décalé).
• Après la dernière itération, \(j\) vaut donc \(-1\), et la clé est replacée en position.

La clé est donc maintenant à l'indice \(0\) et est inférieure à tous les éléments du sous-tableau \([1;k+1]\). On peut donc affirmer que le tableau [0;k+1] est maintenant trié en ordre croissant.

Donc \(P_{k+1}\) est VRAI.

Cas 2 : clé (indice \(k+1\)) supérieure (ou égale) aux éléments de \([0;k]\)

• On ne rentre même pas dans le TANT QUE puisque l'une de ses conditions n'est pas vérifiée :
  TANT QUE j ≥ 0 et que t[j] > cle
• On effectue qu'une seule comparaison entre la clé et l'élément qui le précède. \(j\) vaut donc \(i-1\) après la boucle TANT QUE, et on place la clé avec l'instruction t[j+1] ← cle.
  La clé reste au même indice \(i\).
• Le sous-tableau \([0, k]\) était déjà trié dans l'ordre croissant, on ne le change pas.
• On rajoute la clé (un élément plus grand ou égal à tous les autres) à l'indice \(k+1\).

Finalement, on obtient un sous-tableau \([0; k+1]\) trié après avoir effectué un tour de boucle supplémentaire de la boucle POUR principale.

Donc \(P_{k+1}\) est VRAI.

Cas 3 : clé (indice \(k+1\)) inférieure à certains éléments de \([0;k]\)

Les éléments du sous-tableau \([0;k]\) sont triés, cela signifie que l'on a d'abord une première partie des éléments inférieurs ou égaux à la clé, puis une deuxième partie des éléments supérieurs à la clé.

• Les éléments d'indice \([m;k]\) sont supérieurs à la clé et vont donc être décalés à droite.
• Les éléments d'indice \([0;m-1]\) sont inférieurs ou égaux à la clé et ne vont donc pas bouger.

On rappelle les conditions du TANT QUE : TANT QUE j ≥ 0 et que t[j] > cle

• La seconde condition ne sera vraie que jusqu'à t[m] > cle, on déplace donc d'une case à droite les éléments [m; k] qui vont se retrouver en [m+1; k+1]. L'ordre des éléments n'est pas change (puisqu'on les a juste décalé d'un cran vers la droite).
• Le sous-tableau [0;m-1] ne sera quant à lui pas modifié.
• A l'issue de la boucle, \(j\) contiendra \(m-1\). L'instruction permettant de repositionner la clé au bon endroit est t[j+1] ← cle.
  Donc la clé sera placée à l'indice \(m - 1 + 1 = m\).
• Finalement :
  • Le sous-tableau \([0; m-1]\) est trié (pas de changement) et inférieur ou égal à la clé.
  • La clé est à l'indice \(m\).
  • Le sous-tableau \([m+1;k+1]\) est trié et supérieur à la clé.

Le sous-tableau \([0; k+1]\) est donc bien trié après avoir effectué un tour de boucle supplémentaire.

Donc \(P_{k+1}\) est VRAI.

Terminaison

Il ne reste plus qu'à vérifier la terminaison, c'est-à-dire si l'invariant vérifie toutes les données du tableau d'entrée.

La boucle POUR principale va de 1 à longueur - 1.
L'algorithme aura donc, à la fin, fait longueur - 1 tours de boucle.

Or l'invariant \(P_k\) est la propriété selon laquelle, « Après \(k\) tours de boucle, \(k+1\) éléments sont triés dans le sous-tableau \([0;k]\) de gauche. »

On avait remarqué la relation suivante entre \(i\) et \(k\) : \(k = i\).

À la fin de l'algorithme, \(k\) va donc valoir \(longueur-1\).

Le nombre d'éléments triés correctement est donc \(k + 1 = longueur-1 + 1 = longueur\) élements triés.

Après le dernier tour de boucle, le sous-tableau trié contient donc longueur éléments triés, c'est-à-dire tout le tableau.

La terminaison est démontrée : l'algorithme agit bien sur toutes les données.

Finalement, la proposition \(P_k\) est bien un invariant de la boucle principale de l'algorithme du tri par insertion, et permet de prouver sa correction.