Cours - "Diviser pour régner"¶
Introduction¶
Le principe "diviser pour régner" ("divide and conquer") est un principe militaire ancestrale. Cette stratégie a été mise en avant par Jules César, sous le nom "divide et impera", elle est également reprise également dans les écrits politiques de Nicolas Machiavel.
La méthode "Diviser pour régner" est une approche algorithmique qui repose sur le principe suivant :
Face à un problème généralement complexe, on le divise en une multitude de petits problèmes, avec l'idée que ces "petits problèmes" seront plus simples à résoudre que le problème original. Une fois les petits problèmes résolus, on combine les solutions obtenues pour obtenir la solution du problème initial.
Le paradigme "Diviser pour régner" s'articule donc autour de trois étapes :
- DIVISER : le problème original est fractionné en plusieurs sous-problèmes.
- RÉGNER : on résout individuellement les sous-problèmes, qui sont plus aisés à traiter que le problème initial.
- COMBINER : les solutions des sous-problèmes sont ensuite combinées pour obtenir la solution du problème original.
Les algorithmes basés sur cette approche sont souvent de nature récursive.
Un exemple : Le tri fusion¶
Présentation¶
Rappels de première
En première année, nous avons étudié deux algorithmes de tri peu performants :
- Le tri par sélection, qui présente une complexité quadratique dans le pire cas, le meilleur cas, et en moyenne (le nombre de comparaisons est toujours le même).
- Le tri par insertion, dont la complexité est linéaire dans le meilleur cas, mais quadratique dans le pire cas et en moyenne.
Ces algorithmes ne sont pas couramment utilisés en pratique en raison de leur faible efficacité. En effet, des analyses ont démontré que dans le pire des cas et en moyenne, la meilleure complexité possible pour un algorithme de tri était de \(O(n~log(n))\).
Ceci représente une grande amélioration, car \(log(n)⋘nlog(n)⋘n\). Pour illustrer, considérons les exemples suivants :
- \(log(n) = 10\) pour \(n = 2^{10} = 1024\).
- \(log(n) = 100\) pour \(n = 2^{100} = 1267650600228229401496703205376\).
Cela souligne une différence significative, mettant en évidence l'efficacité accrue de complexités logarithmiques par rapport à linéaires.
Nous allons explorer l'un de ces algorithmes qui applique le principe 'Diviser pour régner' : le tri-fusion.
Le principe du tri fusion
Au lieu de trier la liste entière, nous allons couper la liste en plus petites listes qui seront faciles à trier. On combinera ensuite les petites listes triées obtenues en une seule.

Le tri fusion s’appuie sur le fait que fusionner deux tableaux triés en un tableau trié se fait en un temps linéaire \(O(n)\).
Animation du tri fusion (cliquer ici pour afficher)
Le tableau n'est pas trié
Un exemple de fusion
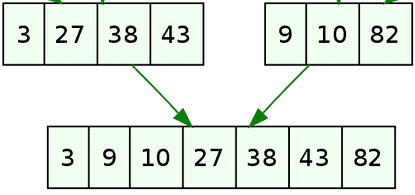
On itère simultanément sur les deux listes, ce qui donne une complexité en \(O(n)\) (linéaire). On procède de la manière suivante :
- On prend en compte 3 et 9, les premiers éléments des deux listes, et on place 3 (le plus petit), puis on avance dans la première liste.
- Puis, avec 27 et 9, on place 9 et on avance dans la deuxième liste.
- L'étape suivante avec 27 et 10 consiste à placer 10, et ainsi de suite.
- Lorsque l'on atteint 27 et 82, on place 27, et ainsi de suite.
- En arrivant à 38 et 82, on place 38.
- Puis, avec 43 et 82, on place 43, constatant ainsi que nous avons parcouru toute la première liste. À ce stade, on place tous les éléments restants de la deuxième liste.
D'un autre côté, la découpe récursive d'un tableau jusqu'à atteindre le cas terminal - un tableau trié d'un seul élément - a une complexité en \(log(n)\). Cela donne une complexité totale de \(O(nlog(n))\), ce qui représente la meilleure performance possible.
Pour améliorer la lisibilité, nous allons diviser notre algorithme en deux fonctions distinctes : l'une pour effectuer la fusion et l'autre pour effectuer le tri (qui effectue le processus de découpage).
- en rouge : diviser
- en bleu : régner
- en vert : fusionner

Implémentation du tri fusion¶
Fusion¶
La fonction fusion(t1, t2) peut s'écrire de la manière suivante :
De manière itérative :
def fusion(t1, t2):
# Initialisation
resultat = []
i, j = 0, 0
# Boucle sur les deux tableaux
while i < len(t1) and j < len(t2):
if t1[i] < t2[j]:
resultat.append(t1[i])
i += 1
else:
resultat.append(t2[j])
j += 1
# Finalisation: On ajoute les éléments restants du tableau non vide restant
# Si t1 n'a pas été entièrement vidé, on ajoute ses éléments restants
if i < len(t1):
for k in range(i, len(t1)):
resultat.append(t1[k])
# Sinon on ajoute les éléments de tbl2 restants
elif j < len(t2):
for k in range(j, len(t2)):
resultat.append(t2[k])
return resultat
La dernière partie de cette algorithme peut se simplifier en utilisant la méthode extend de list :
def fusion(t1, t2):
# Initialisation
resultat = []
i, j = 0, 0
# Boucle sur les deux tableaux
while i < len(t1) and j < len(t2):
if t1[i] < t2[j]:
resultat.append(t1[i])
i += 1
else:
resultat.append(t2[j])
j += 1
# Finalisation: On ajoute les éléments restants du tableau non vide restant
# Si t1 n'a pas été entièrement vidé, on ajoute ses éléments restants
resultat.extend(t1[i:])
resultat.extend(t2[j:])
return resultat
La fonction fusion peut également s'écrire de manière récursive, de la manière suivante :
def fusion(t0, t1):
if not t0:
return t1
if not t1:
return t0
if t0[0] < t1[0]:
return [t0[0]] + fusion(t0[1:], t1)
else:
return [t1[0]] + fusion(t0, t1[1:])
Tri fusion¶
L'algorithme du tri fusion, qui réutilise donc l'algorithme fusion, s'écrit plus facilement de manière récursive :
def tri_fusion(tab):
# Si la taille du tableau est inférieure ou égale à 1, il est déjà trié
if len(tab) <= 1:
return tab
# Diviser le tableau en deux moitiés
milieu = len(tab) // 2
t1 = tab[:milieu]
t2 = tab[milieu:]
# Trier récursivement les deux moitiés
t1_trie = tri_fusion(t1)
t2_trie = tri_fusion(t2)
# Fusionner les deux moitiés triées
resultat = fusion(t1_trie, t2_trie)
return resultat
Vous pouvez tester ce tri ci-dessous :
def fusion(t0, t1):bksl-nl if not t0:bksl-nl return t1bksl-nl if not t1:bksl-nl return t0bksl-nlbksl-nl if t0[0] < t1[0]:bksl-nl return [t0[0]] + fusion(t0[1:], t1)bksl-nl else:bksl-nl return [t1[0]] + fusion(t0, t1[1:])bksl-nl bksl-nldef tripy-undfusion(tab):bksl-nl # Si la taille du tableau est inférieure ou égale à 1, il est déjà triébksl-nl if len(tab) <= 1:bksl-nl return tabbksl-nlbksl-nl # Diviser le tableau en deux moitiésbksl-nl milieu = len(tab) // 2bksl-nl t1 = tab[:milieu]bksl-nl t2 = tab[milieu:]bksl-nlbksl-nl # Trier récursivement les deux moitiésbksl-nl t1py-undtrie = tripy-undfusion(t1)bksl-nl t2py-undtrie = tripy-undfusion(t2)bksl-nlbksl-nl # Fusionner les deux moitiés triéesbksl-nl resultat = fusion(t1py-undtrie, t2py-undtrie)bksl-nlbksl-nl return resultatbksl-nlbksl-nlprint(tripy-undfusion([0, 25, 36, 41, 1, 465, 2, 3, 987]))bksl-nl